New Analysis by
Timothy D. Bilash MD MS OBGYN
www.DrTimDelivers.com
October 27, 2004

in the
Women's Health Initiative Menopause Study (2002)
sponsored by the U.S. Government National Institutes of Health
| WHI index page (10.13.2004/01.01.2008) | ||||||||
| homepage | ||||||||
|
WHI MORTALITY RATES
New Analysis by Timothy D. Bilash MD MS OBGYN www.DrTimDelivers.com October 27, 2004 |
||||||||
 |
||||||||
|
Lower Mortality? with Continuous Estrogen-Progestin
in the Women's Health Initiative Menopause Study (2002) sponsored by the U.S. Government National Institutes of Health |
||||||||
|
An alternative statistical approach applied to the
Women's Health Initiative Estrogen+Progestin Study shows a decreasing Mortality Rate with Continuous Prempro (EP) over time compared to Placebo (PL), which is contrary to the published report. |
|||||
 |
|||||
|
The simple linear model, although limited, provides insight into the
possibility that data anomaly (in Outcome Year4 specifically) decreases the power of the published study findings to find an effect of Estrogen+Progestin on mortality. |
|||||
|
This poster was presented at the
North American Medical Society Annual Meeting (October 6-9, 2004) [Menopause 2004;11(6):664(P-43)] |
|||||
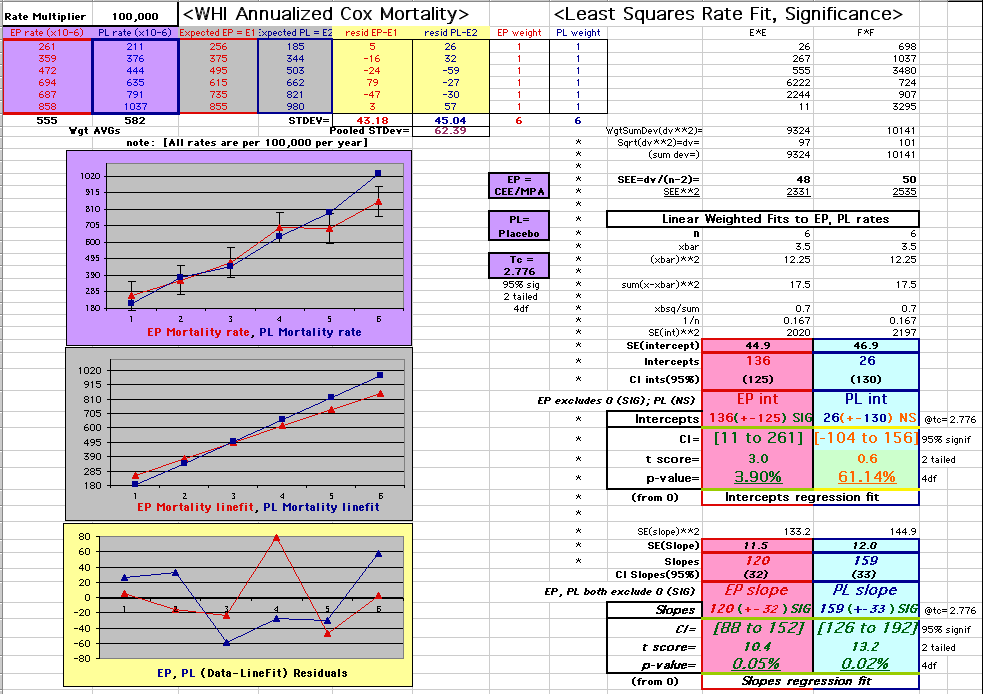
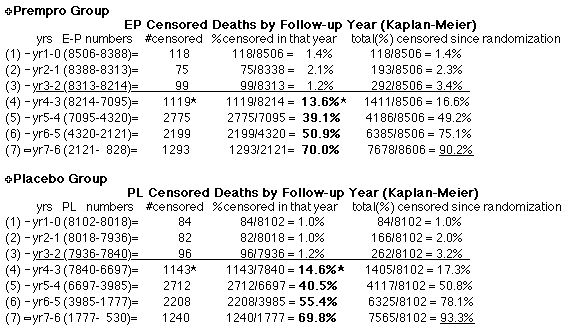
| P43 ABSTRACT Time Dependence of Mortality Rates in the Estrogen Plus Progestin Hormone Replacement Women's Health Initiative (WHI) Study Timothy D Bilash, MD MS North American Menopause Society (NAMS) 15th Annual Meeting October 6-9, 2004, Washington, DC Objective: Perform a statistical analysis of time dependence on the published Mortality Rates from a carefully designed hormone study of daily estrogen (conjugated equine estrogen 0.625mg- CEE) plus progestin (medroxyprogesterone acetate 2.5mg- MPA). Design: The Annualized Cox Mortality Hazard Rates in the Estrogen/Progestin- Treatment(EP) and Placebo(PL) Groups from the published data of the Womens Health Initiative Study [JAMA, July 17, 2002, 288(3):p321-333] are fit using a Least Squares Linear Regression Model for a single Predictor (Hormone Treatment Group) and a single Outcome (Mortality) by Outcome Year, and between-Group slope and intercept differences are obtained. A Student T-Test on the slopes and intercepts of the binary rate data fits, and a Two- Sample T-test on the differences are used as tests of significance. Results: The groups have unweighted linear approximations to the Annualized Mortality Rates (intercept + slope*t) of EP=(136+120*t) and PL=(26+159*t) deaths per 100,000 women at risk per year respectively, where t is the Outcome Year (1 to 6+ years, average 5.2 years). The EP intercept [CI=11to261], EP slope [CI=88to152] and PL slope [CI=126to192] obtained are significant [p<0.04], and the PL intercept [CI=-104to156] is not significant [p=0.6] from 0 by Student T-test using the sample estimates of mean and variance (T=2.78, 4df, 95%CI). The Overall Mortality Rate Difference (OMRD)= EP-PL=(110-39*t) deaths per 100,000 women at risk per year. The slope difference is significant [CI=-76to-2, p=.04], while the intercept difference is not significant [CI=-35to255, p=.12] from 0 by Two-Sample T-test between the Groups (T=2.23, 10df, 95%CI). Conclusion: A statistical analysis of time-dependence on the published Mortality data from the Womens Health Initiative Study is performed, consistent with a time-dependent decrease in Mortality between the Estrogen/Progestin(EP) and Placebo(PL) groups.(c) |
|
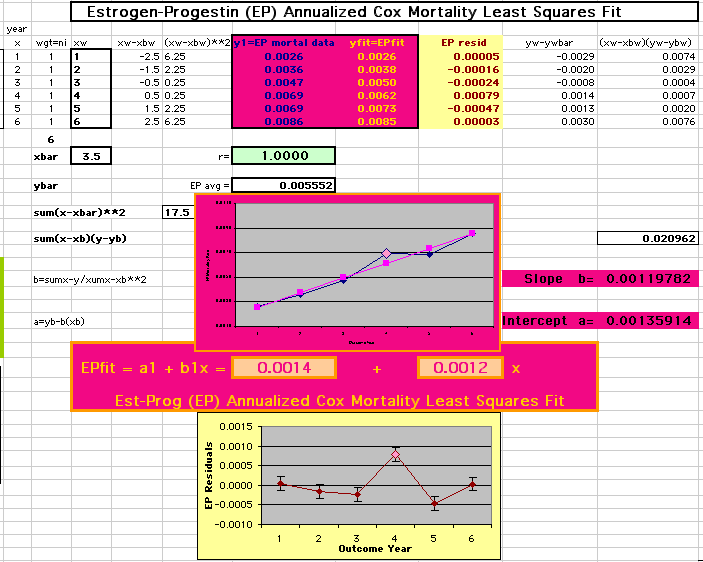
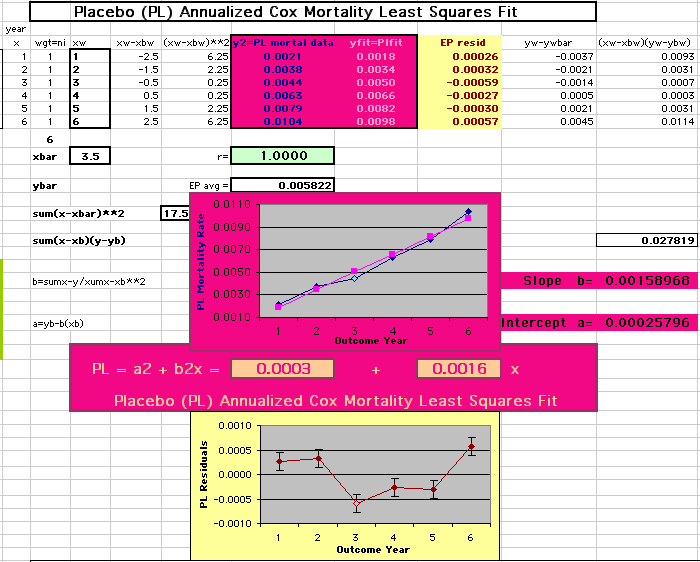
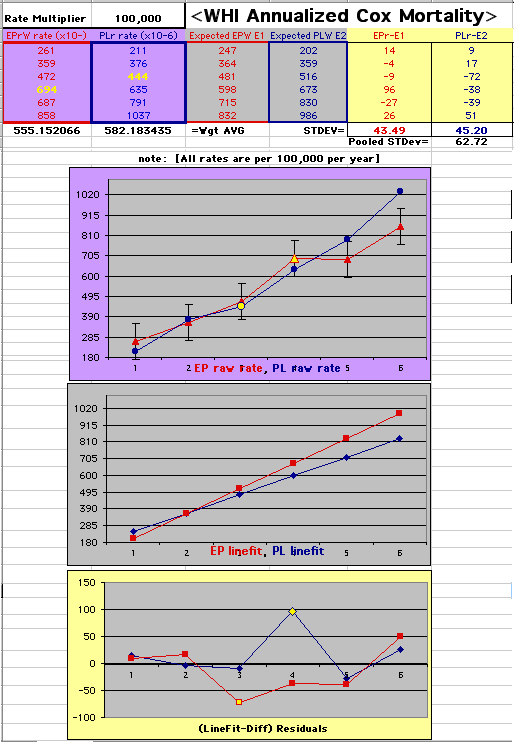
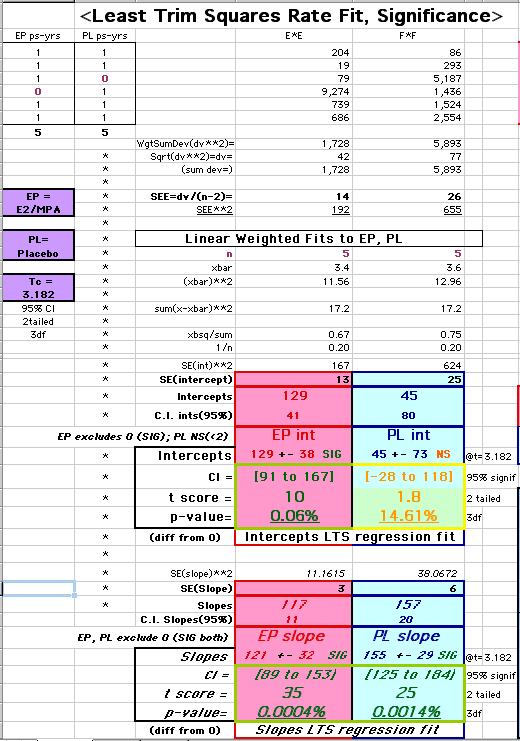
This analysis uses the Least Squares method, which finds the linefit that minimizes the sum of the squared vertical distances between the actual data(y) and predicted fit(Y) values over time. This is done for each study group. (See the discussion of statistics and D&T [13 p195]).
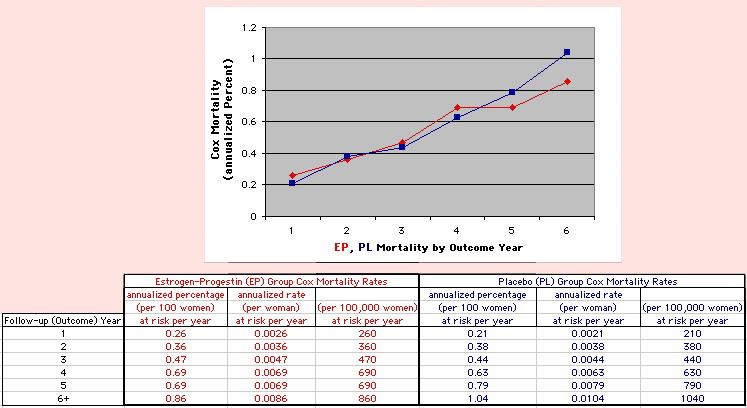
The Annualized Cox Mortality Least Squares Rate Fits obtained by Year for the
Prempro Estrogen-Progestin (EP) and Placebo (PL) Groups are:
|
rate at year 0
INTERCEPT |
rate increase each year
SLOPE |
|||||||||
|
Estrogen-Progestin Group
|
136
26 |
120
159 |
||||||||
| Deaths per 100,000 women at risk per year | ||||||||||
|
Placebo Group
|
||||||||||
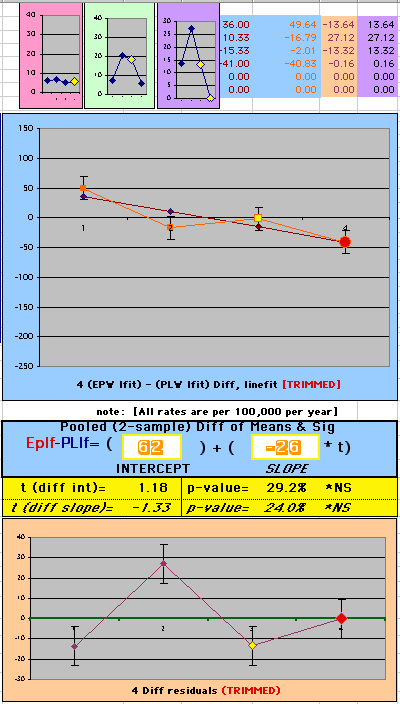
| The Straight Line Fits (EP pink
line
&
gold text
, PL
pink
line
&
pink text
) to the Cox Rates (dkblue line and text) are shown here, with the Residuals [Data-Expected] (brown text , shaded in cream). |
|||
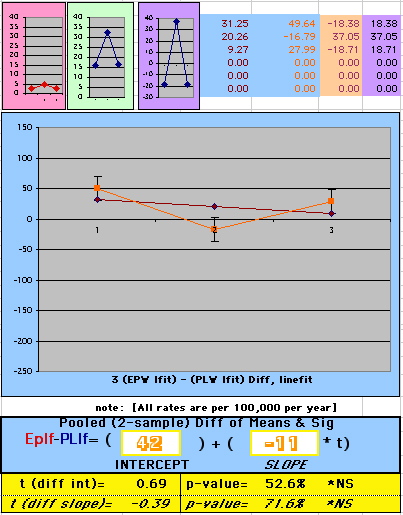
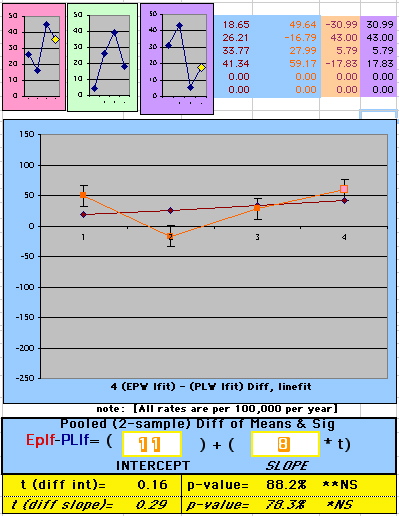
| Because the event rates are low, the data are well approximated by a straight line. Note, however, a large deviation from a straight line fit for Year4 in the EP group (pink diamond). | |||
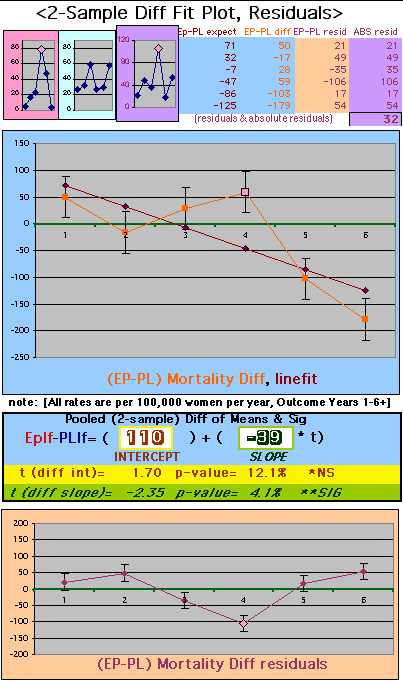
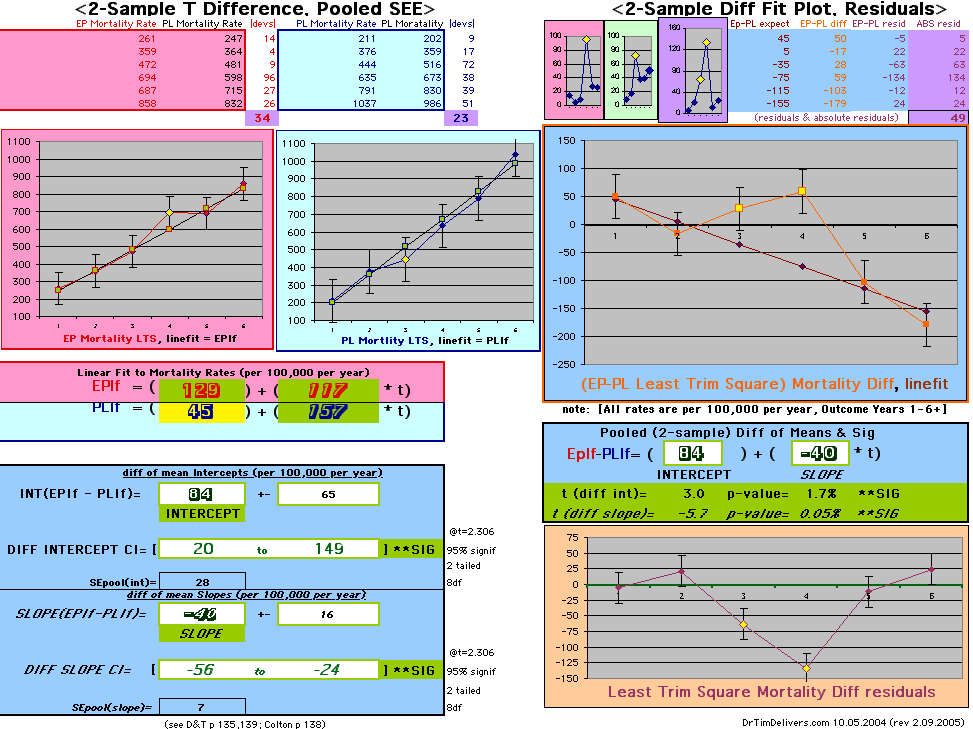
| OMRD = EP-PL = 110 - 39 * [Outcome Year] | |||||
|
Deaths per 100,000 women at risk per year
|
|||||
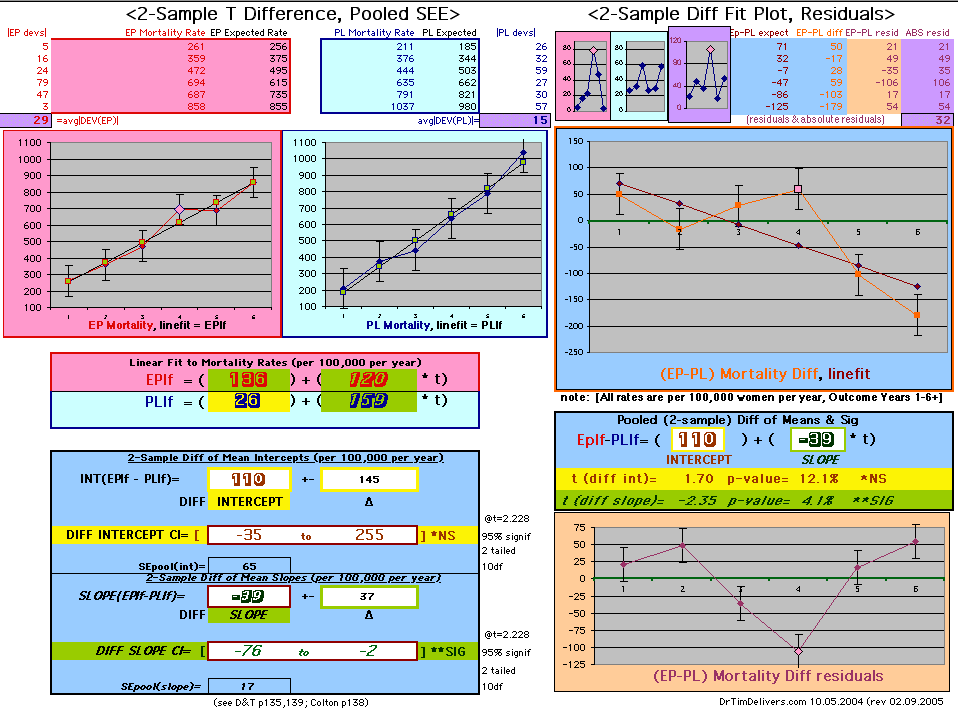
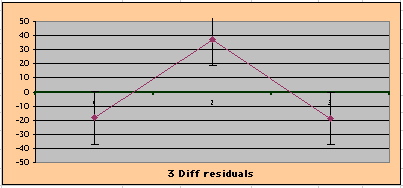
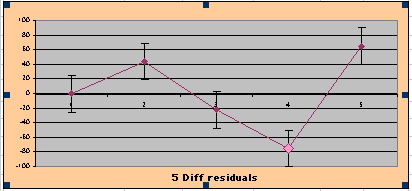
| Note: The Absolute Value of the Residuals are listed top right of the 2-Sample Difference graph. EP Abs(Residuals) are shaded in pink, PL Abs(Residuals) are shaded in pale blue, and the Absolute Value of the Difference of the Residuals |EP-PL| are shaded in purple. | |||
| [click images to enlarge] | |||
|
WHI MORTALITY FITS
|
|||||
|
WHI MORTALITY DIFFERENCE FIT
|
|||||
 |
 |
|
| Timothy Bilash MD OBGYN | www.DrTimDelivers.com | 10.2004 | |||
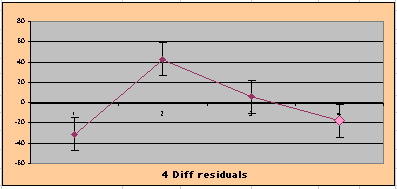
If two groups have the same mortality rates, then the OMRD Difference plot would be expected on average to have a zero Slope and a zero Intercept (
ltblue shading
above). A decreasing slope is found, however. Again note the large Residual for Outcome Year4.
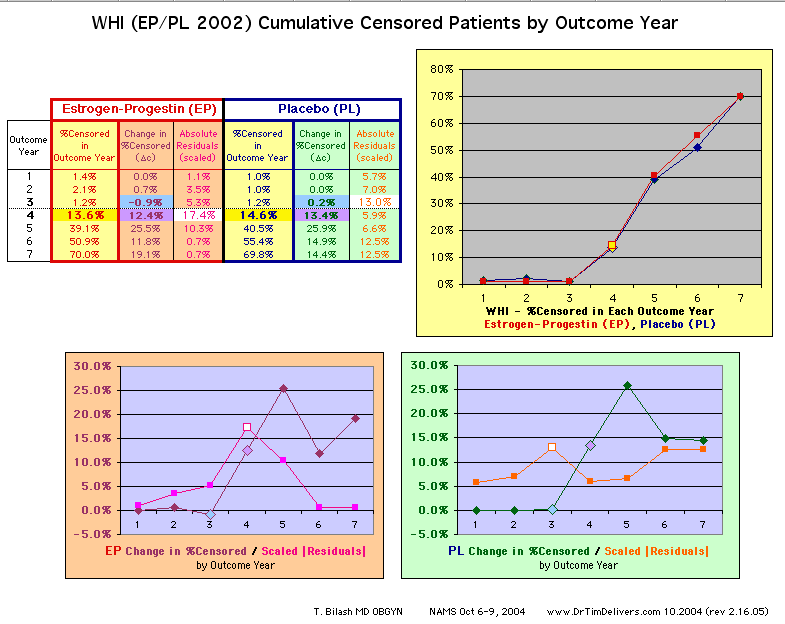
This analysis utilizes the DIFFERENCE, while the WHI reported the RATIO of the Hormone and Placebo Annualized Hazard Rates. Because event rates are low, ratio and difference plots versus time have the same shape. The Ratios of the WHI Cox Annualized Rates by Year (EP/PL in red) are plotted below with the published overall constant Hazard Ratio of HR=.98 (grey line).[1]
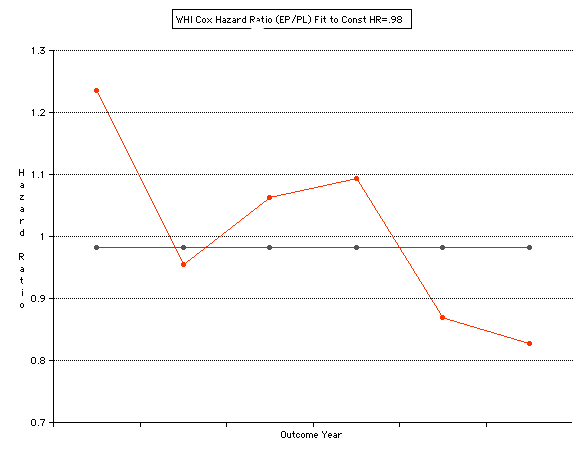
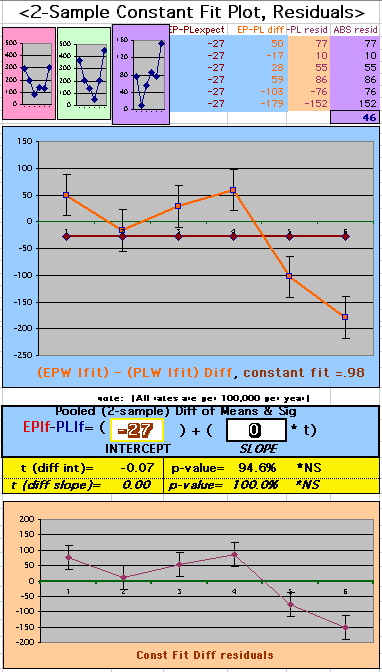
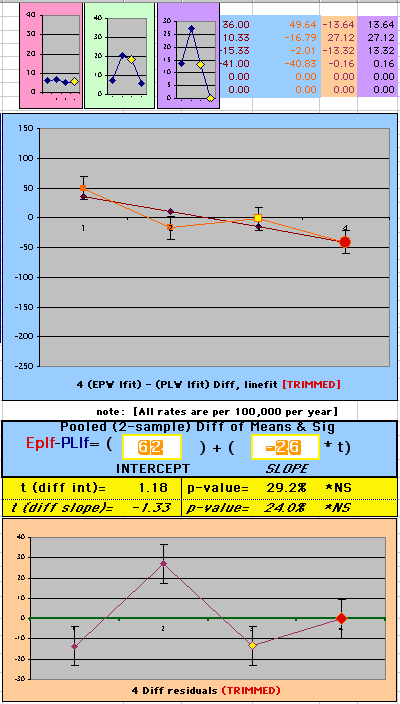
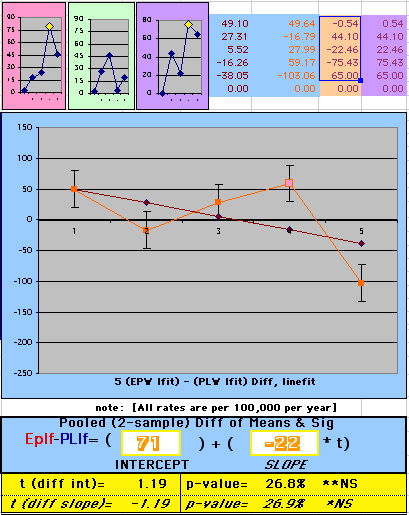
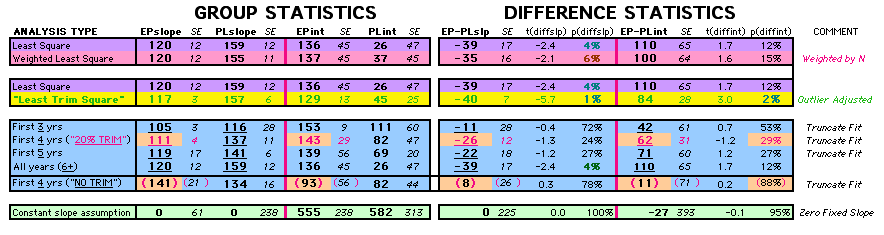
To compare our Least Squares Difference Fit to the published WHI Hazard Ratio (presuming a constant Hazard Ratio or zero difference slope), Least Squares Linefits to the Annual Cox Rates (LS) are calculated assuming equal rate-slopes. The Cox Mortality Rates Data Difference (orange line) and the Least Square Constant Difference Linefit obtained (brown line = constant = -27, zero slope obtained because of assumption of equal slopes) is shown at left. Note that the Residuals for the restricted Constant Difference (purple text, shaded in tan) are larger compared to the unrestricted LS Difference Linefit shown again at right below. They Residuals also do not appear randomly distributed about zero when comparing the Plots of the Residuals (shaded in tan).
|
Difference EP-PL / Constant Slope Linefit
|
Difference EP-PL / Unrestricted Slope Linefit
|
|||
 |
 |
|
 |
 |
 |
|
 |
 |
|||||
 |
||||||
 |
||||||
 |
 |
|||||
 |
|||
 |
|||
 |
|||
 |
||